Metrics explained

Contents

The minimal pair ABX task ( , & al., , , , , & (). Evaluating speech features with the minimal-pair ABX task: Analysis of the classical MFC/PLP pipeline. ) , ( , & al., , , , , & (). Evaluating speech features with the minimal-pair ABX task (II): Resistance to noise. ) is inspired by match-to-sample tasks used in human psychophysics and is a simple way to measure discriminability between two sound categories (where the sounds a and b belong to different categories $\mathbf{A}$ and $\mathbf{B}$, respectively, and the task is to decide whether the sound x belongs to one or the other). It does not require any training and only requires to define a dissimilarity d between the representations of speech tokens.

In Task 1, we measure the discriminability of phoneme categories in submitted representations, for all the pairs of phonemes present in the gold phonemic transcription for the test set.

ABX Discriminability

We define the ABX Discriminability of category $\mathbf{A}$ from category $\mathbf{B}$ as the probability that a and x are further apart than b and x according to some distance d over the (model-dependent) representations for these sounds when a and x are from category $\mathbf{A}$ and b is from category $\mathbf{B}$.

Given a set of sounds $S(\mathbf{A})$ from category $\mathbf{A}$ and a set of sounds $S(\mathbf{B})$ from category $\mathbf{y}$, we estimate this probability using the following formula:

$$ \begin{array}{rcl} \hat{\theta}(\mathbf{A}, \mathbf{B}) & := & \frac{1}{m(m-1)n} \sum_{a\in S(\mathbf{A})} \sum_{b\in S(\mathbf{B})} \sum_{x\in S(\mathbf{A}) \setminus {a}}\\ & & ~~~~~~~~~~~~~~~~~~~~~~\mathbb{1}\left\{d(a,x)<d(b,x)\right\} \\ & & ~~~~~~~~~~~~~~~~ + \frac{1}{2}\mathbb{1}\left\{d(a,x)=d(b,x)\right\} \end{array} $$

where $m$ and $n$ are the number of sounds in $S(\mathbf{A})$ and $S(\mathbf{B})$ and $\mathbb{1}$ denotes an indicator function.

Note that $\hat{\theta}(\mathbf{A}, \mathbf{B}) $ is asymmetric over the two categories. We obtain a symmetric measure $\hat\theta_\mathrm{symm}$ by taking the average of the ABX discriminability of $\mathbf{A}$ from $\mathbf{B}$ and of $\mathbf{B}$ from $\mathbf{A}$.

Calculating the distance d

We do not require $d$ to be a metric in the mathematical sense. The default distances provided in this benchmark are based on DTW divergences with the underlying frame-to-frame distance being either angular distance (arc cos of normalized dot-product) or KL-divergence.

For most systems, the angular distance usually gives good results, and for others (posteriorgrams) the KL distance is more appropriate. Participants can experiment with their own distance functions if they wish, as long as it was not obtained through supervised training.

ABX Phoneme Discriminability benchmarks

In the ABX Phoneme Discriminability measure, the categories whose discriminability is measured are phonemes.

A list of stimuli is obtained by examining the entire benchmark corpus and finding the timestamps of all phonemes from the gold transcription (typically obtained by forced alignment). The timestamps are taken either with the surrounding triphone or as isolated phonemes. These are used to construct all possible $\mathbf{A,B,X}$ triplets. See below under Types of ABX Phoneme Discrimination tasks for details.

The benchmark files are entire utterances, and the task of participants is to provide these files in their learned representations at a fixed frame rate. The evaluation uses the timestamps in its list to index back into the learned representations.

In practice, we present the overall error rate (lower is better), rather than an overall discriminability. The scores are averages of averages. See the explanation for each condition below under Types of ABX Phoneme Discrimination tasks.

Relationship with other metrics

As shown in Schatz ( , (). ABX-discriminability measures and applications  (Doctoral dissertation). École Normale Supérieure ) , ABX is an unbiased statistically efficient metric of discriminability (compared to supervised methods like LDA, or unsupervised ones like kmeans and KNN) and can be seen as good predictor of the result of an unsupervised clustering method.

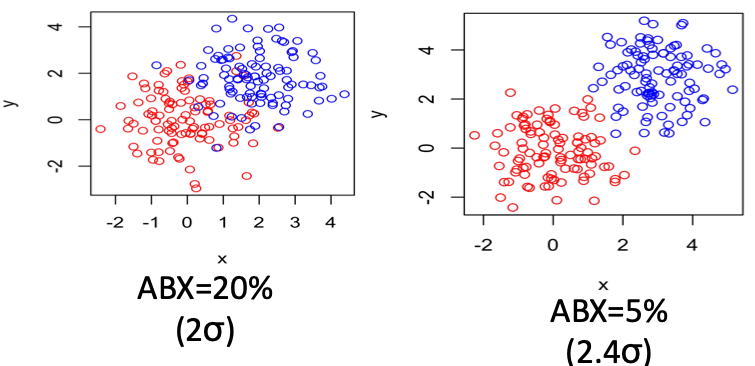
Figure. 2. Illustration of category discriminability for different values of ABX.

Types of ABX Phoneme Discrimination benchmarks

For older benchmarks (abx15, abx17, and abxLS), items have timestamps which include a small amount of surrounding context. In particular, each phoneme token begins at the beginning of the preceding phone, and ends at the end of the following phone (triphone timestamps).

For the abxLSPhon benchmark, items are isolated phonemes.

  • Comparing within-speaker and across-speaker scores allows us to evaluate the units’ invariance to speaker.
  • Comparing within-context and any-context scores allows us to evaluate the units’ invariance to context. The any-context condition is only available in the abxLSPhon benchmark. All other benchmarks are exclusively within-context.
  • The zrc2017 dataset, used by the abx17 benchmark, is split into 120s, 10s, and 1s files. Comparing scores on these conditions allows us to evaluate the efficiency with which systems adapt to talkers.
  • The abxLS dataset (the dataset used by the abxLS and abxLSPhon benchmarks) is split into clean and other subsets, which are derived from the amount of filtering done on the source LibriSpeech corpus. Comparing the scores on clean with the slightly more difficult other set allows us to evaluate general robustness to miscellaneous variation in listening conditions.

Below we explain how the aggregate scores are calculated in each condition.

Within-speaker, within-context

The error rate is $1-\hat\theta_\mathrm{overall}$, where $\theta_\mathrm{overall}$ is:

  • The average over all pairs of phonemes $\mathbf{A,B}$ (e.g., /æ/ vs /i/) of …
    • the average over all triphone contexts $c$ (e.g., /r_d/, /a_f/, etc) of …
      • the average over all speakers $s$ …
        • $\hat\theta_\mathrm{symm}(\mathbf{A,B})$ calculated over all triplets with speaker $s$ in context $c$

Across-speaker, within-context

The error rate is $1-\hat\theta_\mathrm{overall}$, where $\theta_\mathrm{overall}$ is:

  • The average over all pairs of phonemes $\mathbf{A,B}$ (e.g., /æ/ vs /i/) of …
    • the average over all triphone contexts $c$ (e.g., /r_d/, /a_f/, etc) of …
      • the average over all pairs of speakers $s,t$ …
        • $\hat\theta_\mathrm{symm}(\mathbf{A,B})$ calculated over all triplets in context $c$ for which $\mathbf{A,B}$ are speaker $s$ and $\mathbf{X}$ is speaker $t$

Within-speaker, any-context

The error rate is $1-\hat\theta_\mathrm{overall}$, where $\theta_\mathrm{overall}$ is:

  • The average over all pairs of phonemes $\mathbf{A,B}$ (e.g., /æ/ vs /i/) of …
    • the average over all speakers $s$ …
      • $\hat\theta_\mathrm{symm}(\mathbf{A,B})$ calculated over all triplets with speaker $s$

Across-speaker, any-context

The error rate is $1-\hat\theta_\mathrm{overall}$, where $\theta_\mathrm{overall}$ is:

  • The average over all pairs of phonemes $\mathbf{A,B}$ (e.g., /æ/ vs /i/) of …
    • the average over all pairs of speakers $s,t$ …
      • $\hat\theta_\mathrm{symm}(\mathbf{A,B})$ calculated over all triplets for which $\mathbf{A,B}$ are speaker $s$ and $\mathbf{X}$ is speaker $t$

Cited

Schatz, Peddinti, Bach, Jansen, Hermansky & Dupoux (2013)
, , , , & (). Evaluating speech features with the minimal-pair ABX task: Analysis of the classical MFC/PLP pipeline.
Schatz, Peddinti, Cao, Bach, Hermansky & Dupoux (2014)
, , , , & (). Evaluating speech features with the minimal-pair ABX task (II): Resistance to noise.
Schatz (2016)
(). ABX-discriminability measures and applications  (Doctoral dissertation). École Normale Supérieure